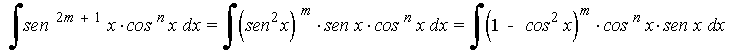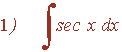CALCULO INTEGRAL
PORTAFOLIO DE LA MATERIA CALCULO INTEGRAL - SISTEMAS DE INFORMACION Hecho por Gustavo Jimenez
BUSCAR ALGO RELACIONADO CON CALCULO INTEGRAL:
4 mar 2021
Materia
DIFERENCIAL E INTEGRAL DEFINIDA
 es una función derivable, la diferencial de una función correspondiente al incremento
es una función derivable, la diferencial de una función correspondiente al incremento  de la variable independiente, es el producto
de la variable independiente, es el producto  .
.La diferencial de una función se representa por  ó
ó  .
.




La diferencial en un punto representa el incremento de la ordenada de la tangente, correspondiente a un incremento de la variable independiente.
- 1. Proyecto de cálculo diferencial e integral en contexto: En este enfoque se plantea que el cálculo es un lenguaje, una red de conceptos y un conjunto de técnicas. La metodología consiste en el planteamiento de problemas y situaciones reales, el estudiantado trabaja en grupos pequeños. Los problemas se abordan inicialmente con métodos numéricos y con la ayuda de la computadora. Posteriormente, se plantean soluciones analíticas. De esta manera se construyen finalmente los conceptos del cálculo diferencial e integral.
- 2. Proyecto de debate científico: En este enfoque se introducen los conceptos del cálculo diferencial e integral mediante la presentación de problemas científicos, de este modo, el estudiantado trabaja como si fuese matemático, para ello, debe formular preguntas, hacer conjeturas y realizar discusiones con el resto de pares de la clase.
- 3. Ingeniería didáctica: Se propone una investigación que consta de tres etapas, a saber, análisis e interpretación de la enseñanza, análisis de las restricciones en la enseñanza; el diseño de una ingeniería didáctica.
La sumatoria o sumatorio (llamada también notación sigma ) es una operación matemática que se emplea para calcular la suma de muchos o infinitos sumandos.
La operación sumatoria se expresa con la letra griega sigma mayúscula Σ, y se representa así:
Expresión que se lee: " sumatoria de Xi, donde i toma los valores desde 1 hasta n ".
i es el valor inicial, llamado límite inferior.
n es el valor final, llamado límite superior.
Pero necesariamente debe cumplirse que:
i ≤ n
Si la sumatoria abarca la totalidad de los valores, entonces no se anotan sus límites y su expresión se puede simplificar:
1.5. LA INTEGRAL DEFINIDA Y SUS PROPIEDADES
La integral definida es un concepto utilizado para determinar el valor de las áreas limitadas por curvas y rectas. Dado el intervalo [a, b] en el que, para cada uno de sus puntos x, se define una función f (x) que es mayor o igual que 0 en [a, b], se llama integral definida de la función entre los puntos a y b al área de la porción del plano que está limitada por la función, el eje horizontal OX y las rectas verticales de ecuaciones x = a y x = b.
La integral definida de la función entre los extremos del intervalo [a, b] se denota como:
Propiedades de la integral definida
La integral definida cumple las siguientes propiedades:
- Toda integral extendida a un intervalo de un solo punto, [a, a], es igual a cero.
- Cuando la función f (x) es mayor que cero, su integral es positiva; si la función es menor que cero, su integral es negativa.
- La integral de una suma de funciones es igual a la suma de sus integrales tomadas por separado.
- La integral del producto de una constante por una función es igual a la constante por la integral de la función (es decir, se puede «sacar» la constante de la integral).
- Al permutar los límites de una integral, ésta cambia de signo.
- Dados tres puntos tales que a < b < c, entonces se cumple que (integración a trozos):
- Para todo punto x del intervalo [a,b] al que se aplican dos funciones f (x) y g (x) tales que f (x) £ g (x), se verifica que:
DIFERENCIAL E INTEGRAL DEFINIDA II
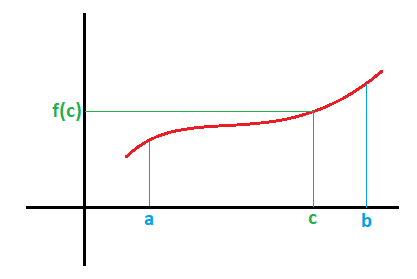
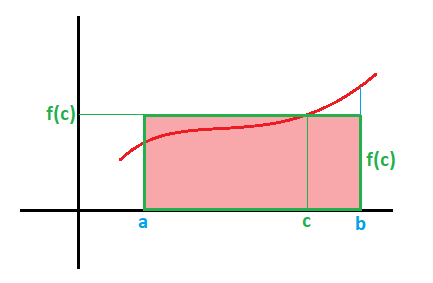
1.6. EL TEOREMA DEL VALOR MEDIO PARA INTEGRALES
Si tenemos una función definida en un intervalo [a,b], el área limitada por la función y los rectas x=a y x=b es la siguiente:
1.7. TEOREMA FUNDAMENTAL DEL CALCULO
El teorema fundamental del cálculo dice que la derivada de la integral  de la función continua
de la función continua  es la propia
es la propia  .
.

El teorema fundamental del cálculo dice que la derivada de la integral  de la función continua
de la función continua  es la propia
es la propia  .
.

El teorema fundamental del cálculo nos indica que la derivación y la integración son operaciones inversas.
Al integrar una función continua y luego derivarla se recupera la función original.
Ejemplo:
Hallar la derivada de

1Notamos que  , por lo que su diferencial
, por lo que su diferencial 
2Aplicando el teorema fundamental del cálculo tenemos

1.8. METODO DE SUSTITUCIÓN
Ejemplo de un sistema:
{3x+2y=1x−5y=6
Es un sistema de dos ecuaciones con dos incógnitas (x e y.
consiste en despejar o aislar una de las incógnitas (por ejemplo, x) y sustituir su expresión en la otra ecuación. De este modo, obtendremos una ecuación de primer grado con la otra incógnita, y. Una vez resuelta, calculamos el valor de x sustituyendo el valor de y que ya conocemos.
1.9. INTEGRACION POR PARTES
La fórmula de la integración por partes es

Observemos que tenemos que derivar  e integrar
e integrar  , por lo que será conveniente que la integral de
, por lo que será conveniente que la integral de  sea sencilla.
sea sencilla.
En general, las funciones polinómicas, logarítmicas y arcotangente se eligen como  . Mientras que las funciones exponenciales, seno y coseno se eligen como
. Mientras que las funciones exponenciales, seno y coseno se eligen como  .
.
La fórmula de la integración por partes es

Observemos que tenemos que derivar  e integrar
e integrar  , por lo que será conveniente que la integral de
, por lo que será conveniente que la integral de  sea sencilla.
sea sencilla.
En general, las funciones polinómicas, logarítmicas y arcotangente se eligen como  . Mientras que las funciones exponenciales, seno y coseno se eligen como
. Mientras que las funciones exponenciales, seno y coseno se eligen como  .
.
Deducción de la fórmula
Supongamos que tenemos las funciones  y
y  . Entonces su derivada está dada por
. Entonces su derivada está dada por
![Rendered by QuickLaTeX.com \displaystyle \left[ u(x) \cdot v(x) \right]' = u'(x) \cdot v(x) + u(x) \cdot v'(x)](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-ca4bd8ef82244203e4d564192a6edc9d_l3.png)
Si integramos ambos lados de la ecuación, obtenemos
![Rendered by QuickLaTeX.com \begin{align*} u(x) \cdot v(x) & = \int{\left[ u(x) \cdot v(x) \right]'}dx\\& = \int{\left( u'(x) \cdot v(x) + u(x) \cdot v'(x) \right)}dx\\& = \int{u'(x)v(x)}dx + \int{u(x)v'(x)}dx\end{align*}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-60cb720701c35da66fbe5ce45c2a789e_l3.png)
Luego, si pasamos  al lado izquierdo, obtenemos
al lado izquierdo, obtenemos

que es la fórmula que buscábamos
1.10. INTEGRALES QUE INCLUYEN POTENCIAS DE SENO Y COSENO
La potencia del seno es impar y positiva. En este caso conservamos un factor seno y se pasan los restantes factores a coseno:
Veremos un método para la resolución de integrales cuyo integrando es una potencia de una función seno o coseno ó el producto de estas.
Considere la integral de la forma
Supongamos que tenemos las funciones  y
y  . Entonces su derivada está dada por
. Entonces su derivada está dada por
![Rendered by QuickLaTeX.com \displaystyle \left[ u(x) \cdot v(x) \right]' = u'(x) \cdot v(x) + u(x) \cdot v'(x)](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-ca4bd8ef82244203e4d564192a6edc9d_l3.png)
Si integramos ambos lados de la ecuación, obtenemos
![Rendered by QuickLaTeX.com \begin{align*} u(x) \cdot v(x) & = \int{\left[ u(x) \cdot v(x) \right]'}dx\\& = \int{\left( u'(x) \cdot v(x) + u(x) \cdot v'(x) \right)}dx\\& = \int{u'(x)v(x)}dx + \int{u(x)v'(x)}dx\end{align*}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-60cb720701c35da66fbe5ce45c2a789e_l3.png)
Luego, si pasamos  al lado izquierdo, obtenemos
al lado izquierdo, obtenemos

que es la fórmula que buscábamos
1.10. INTEGRALES QUE INCLUYEN POTENCIAS DE SENO Y COSENO
La potencia del seno es impar y positiva. En este caso conservamos un factor seno y se pasan los restantes factores a coseno:
Veremos un método para la resolución de integrales cuyo integrando es una potencia de una función seno o coseno ó el producto de estas.
Considere la integral de la forma
Ejemplo:
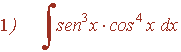
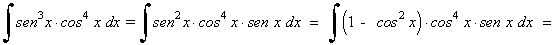
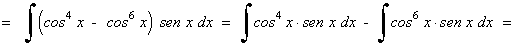
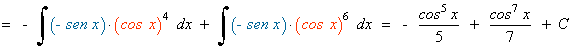
La potencia del coseno es impar y positiva. En este caso conservamos un factor coseno y se pasan los restantes factores a seno:
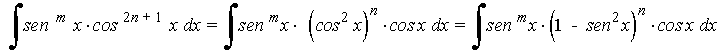
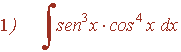
![]()
![]()
![]()
La potencia del coseno es impar y positiva. En este caso conservamos un factor coseno y se pasan los restantes factores a seno:
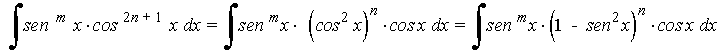
Ejemplo:
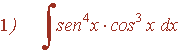
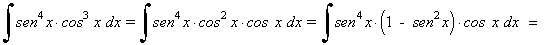
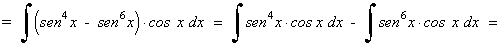
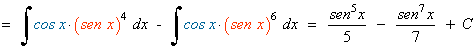
Las potencias del seno y del coseno son impares y positivas. En este caso conservamos un factor del seno o del coseno y se pasan los restantes factores al seno o al coseno:
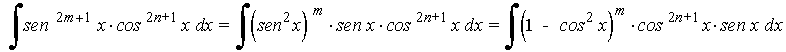
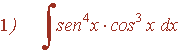
![]()
![]()
![]()
Las potencias del seno y del coseno son impares y positivas. En este caso conservamos un factor del seno o del coseno y se pasan los restantes factores al seno o al coseno:
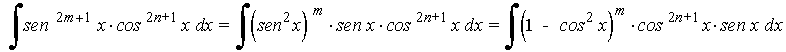
Ejemplo:
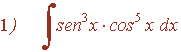
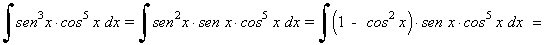
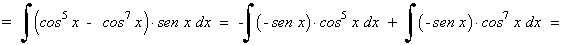
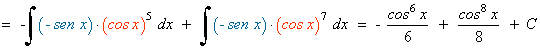
1.11. INTEGRALES QUE CONTIENEN POTENCIAS DE SECANTE Y TANGENTE
La potencia de la secante es par y positiva (2n) conservamos un factor de sec2x y se usa la fórmula sec2x = 1 + tg2x para expresar los demás factores en términos de tg x :
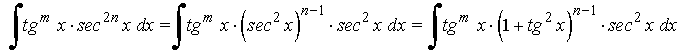
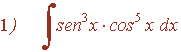
![]()
![]()
![]()
La potencia de la secante es par y positiva (2n) conservamos un factor de sec2x y se usa la fórmula sec2x = 1 + tg2x para expresar los demás factores en términos de tg x :
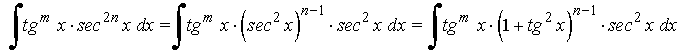
Ejemplo:
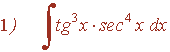
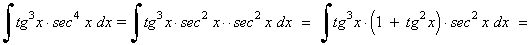
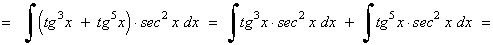
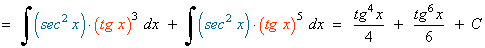
La potencia de la tangente es impar y positiva (2m+1) conservamos un factor de sec x·tg x y se usa la fórmula tg2x = sec2x - 1 para expresar los demás factores en términos de sec x :
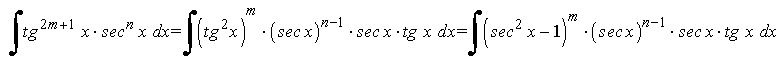
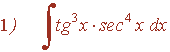
![]()
![]()
![]()
La potencia de la tangente es impar y positiva (2m+1) conservamos un factor de sec x·tg x y se usa la fórmula tg2x = sec2x - 1 para expresar los demás factores en términos de sec x :
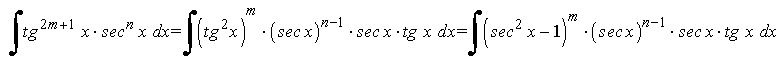
Ejemplo:
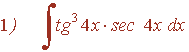
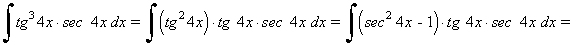
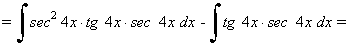
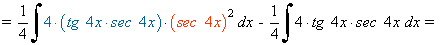
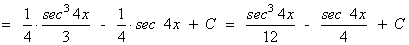
La potencia de la tangente es par y positiva (2m) y no hay secante convertimos un factor tg2x en términos de sec2x . Se desarrolla y se repite si es necesario:
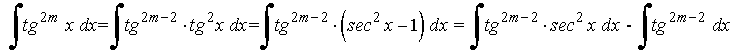
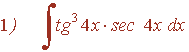
![]()
![]()
![]()
![]()
La potencia de la tangente es par y positiva (2m) y no hay secante convertimos un factor tg2x en términos de sec2x . Se desarrolla y se repite si es necesario:
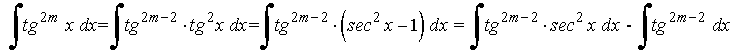
Ejemplo:
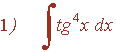
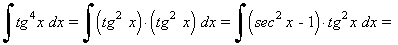
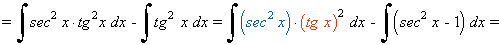
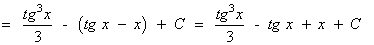
La potencia de la tangente es impar y positiva (2m+1) y no hay secante convertimos un factor tg2x en términos de sec2x . Se desarrolla y se repite si es necesario:
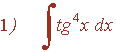
![]()
![]()
![]()
La potencia de la tangente es impar y positiva (2m+1) y no hay secante convertimos un factor tg2x en términos de sec2x . Se desarrolla y se repite si es necesario:
Ejemplo:
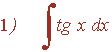
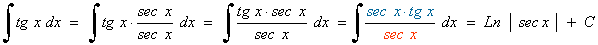
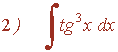
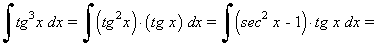
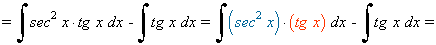
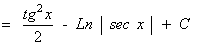
La potencia de la secante es impar y positiva (2n+1) y no hay tangente se resuelve por partes:
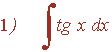
![]()
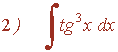
![]()
![]()
![]()
La potencia de la secante es impar y positiva (2n+1) y no hay tangente se resuelve por partes:
Ejemplo:
-
2.7. INTEGRALES BINOMIAS Se trata de integrales de la forma: que incluye integrales de raíces cuadradas (p = 1/2 ), de raíces cúbicas (p = ...
-
2.3 SUSTITUCION TRIGONOMETRICA Primer caso. Para el caso de la expresión , se realizará la sustitución siguiente utilizando como “u” una n...
-
2.2 INTEGRALES DE POTENCIAS DE FUNCIONES HIPERBOLICAS Las funci ones hiperbólicas son análogas a las funciones ordinarias . Las funciones h...