1.6. EL TEOREMA DEL VALOR MEDIO PARA INTEGRALES
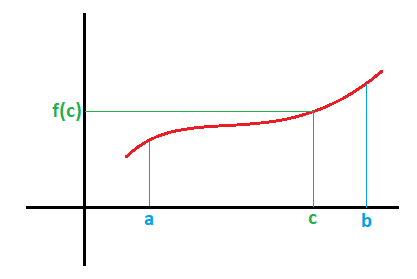
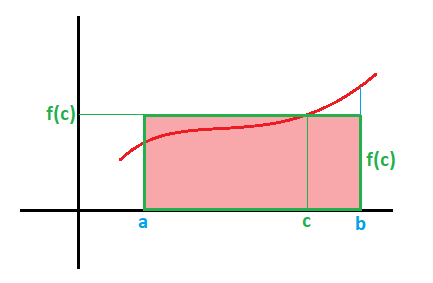
Si tenemos una función definida en un intervalo [a,b], el área limitada por la función y los rectas x=a y x=b es la siguiente:
1.7. TEOREMA FUNDAMENTAL DEL CALCULO
El teorema fundamental del cálculo dice que la derivada de la integral  de la función continua
de la función continua  es la propia
es la propia  .
.

El teorema fundamental del cálculo dice que la derivada de la integral  de la función continua
de la función continua  es la propia
es la propia  .
.

El teorema fundamental del cálculo nos indica que la derivación y la integración son operaciones inversas.
Al integrar una función continua y luego derivarla se recupera la función original.
Ejemplo:
Hallar la derivada de

1Notamos que  , por lo que su diferencial
, por lo que su diferencial 
2Aplicando el teorema fundamental del cálculo tenemos

1.8. METODO DE SUSTITUCIÓN
Ejemplo de un sistema:
Es un sistema de dos ecuaciones con dos incógnitas ( e .
consiste en despejar o aislar una de las incógnitas (por ejemplo, ) y sustituir su expresión en la otra ecuación. De este modo, obtendremos una ecuación de primer grado con la otra incógnita, . Una vez resuelta, calculamos el valor de sustituyendo el valor de que ya conocemos.
1.9. INTEGRACION POR PARTES
La fórmula de la integración por partes es

Observemos que tenemos que derivar  e integrar
e integrar  , por lo que será conveniente que la integral de
, por lo que será conveniente que la integral de  sea sencilla.
sea sencilla.
En general, las funciones polinómicas, logarítmicas y arcotangente se eligen como  . Mientras que las funciones exponenciales, seno y coseno se eligen como
. Mientras que las funciones exponenciales, seno y coseno se eligen como  .
.
La fórmula de la integración por partes es

Observemos que tenemos que derivar  e integrar
e integrar  , por lo que será conveniente que la integral de
, por lo que será conveniente que la integral de  sea sencilla.
sea sencilla.
En general, las funciones polinómicas, logarítmicas y arcotangente se eligen como  . Mientras que las funciones exponenciales, seno y coseno se eligen como
. Mientras que las funciones exponenciales, seno y coseno se eligen como  .
.
Deducción de la fórmula
Supongamos que tenemos las funciones  y
y  . Entonces su derivada está dada por
. Entonces su derivada está dada por
![Rendered by QuickLaTeX.com \displaystyle \left[ u(x) \cdot v(x) \right]' = u'(x) \cdot v(x) + u(x) \cdot v'(x)](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-ca4bd8ef82244203e4d564192a6edc9d_l3.png)
Si integramos ambos lados de la ecuación, obtenemos
![Rendered by QuickLaTeX.com \begin{align*} u(x) \cdot v(x) & = \int{\left[ u(x) \cdot v(x) \right]'}dx\\& = \int{\left( u'(x) \cdot v(x) + u(x) \cdot v'(x) \right)}dx\\& = \int{u'(x)v(x)}dx + \int{u(x)v'(x)}dx\end{align*}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-60cb720701c35da66fbe5ce45c2a789e_l3.png)
Luego, si pasamos  al lado izquierdo, obtenemos
al lado izquierdo, obtenemos

que es la fórmula que buscábamos
1.10. INTEGRALES QUE INCLUYEN POTENCIAS DE SENO Y COSENO
La potencia del seno es impar y positiva. En este caso conservamos un factor seno y se pasan los restantes factores a coseno:
Veremos un método para la resolución de integrales cuyo integrando es una potencia de una función seno o coseno ó el producto de estas.
Considere la integral de la forma
Supongamos que tenemos las funciones  y
y  . Entonces su derivada está dada por
. Entonces su derivada está dada por
![Rendered by QuickLaTeX.com \displaystyle \left[ u(x) \cdot v(x) \right]' = u'(x) \cdot v(x) + u(x) \cdot v'(x)](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-ca4bd8ef82244203e4d564192a6edc9d_l3.png)
Si integramos ambos lados de la ecuación, obtenemos
![Rendered by QuickLaTeX.com \begin{align*} u(x) \cdot v(x) & = \int{\left[ u(x) \cdot v(x) \right]'}dx\\& = \int{\left( u'(x) \cdot v(x) + u(x) \cdot v'(x) \right)}dx\\& = \int{u'(x)v(x)}dx + \int{u(x)v'(x)}dx\end{align*}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-60cb720701c35da66fbe5ce45c2a789e_l3.png)
Luego, si pasamos  al lado izquierdo, obtenemos
al lado izquierdo, obtenemos

que es la fórmula que buscábamos
1.10. INTEGRALES QUE INCLUYEN POTENCIAS DE SENO Y COSENO
La potencia del seno es impar y positiva. En este caso conservamos un factor seno y se pasan los restantes factores a coseno:
Veremos un método para la resolución de integrales cuyo integrando es una potencia de una función seno o coseno ó el producto de estas.
Considere la integral de la forma
Ejemplo:
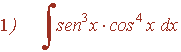
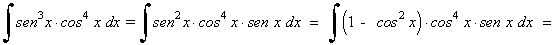
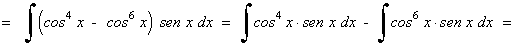
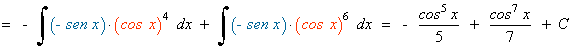
La potencia del coseno es impar y positiva. En este caso conservamos un factor coseno y se pasan los restantes factores a seno:
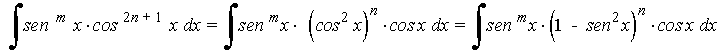
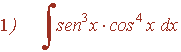
![]()
![]()
![]()
La potencia del coseno es impar y positiva. En este caso conservamos un factor coseno y se pasan los restantes factores a seno:
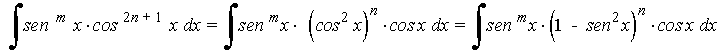
Ejemplo:
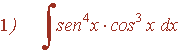
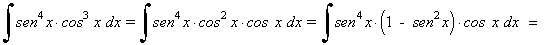
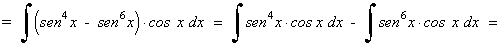
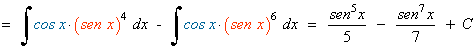
Las potencias del seno y del coseno son impares y positivas. En este caso conservamos un factor del seno o del coseno y se pasan los restantes factores al seno o al coseno:
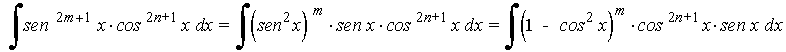
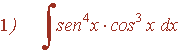
![]()
![]()
![]()
Las potencias del seno y del coseno son impares y positivas. En este caso conservamos un factor del seno o del coseno y se pasan los restantes factores al seno o al coseno:
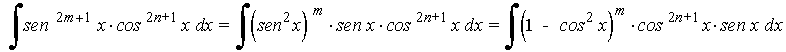
Ejemplo:
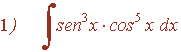
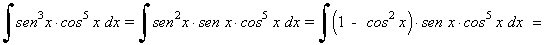
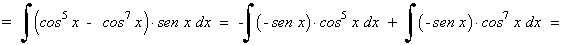
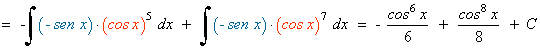
1.11. INTEGRALES QUE CONTIENEN POTENCIAS DE SECANTE Y TANGENTE
La potencia de la secante es par y positiva (2n) conservamos un factor de sec2x y se usa la fórmula sec2x = 1 + tg2x para expresar los demás factores en términos de tg x :
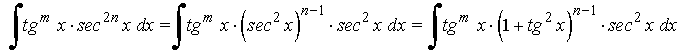
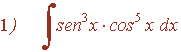
![]()
![]()
![]()
La potencia de la secante es par y positiva (2n) conservamos un factor de sec2x y se usa la fórmula sec2x = 1 + tg2x para expresar los demás factores en términos de tg x :
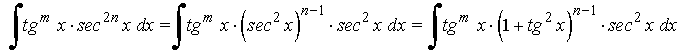
Ejemplo:
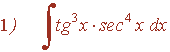
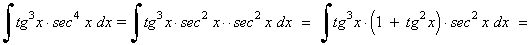
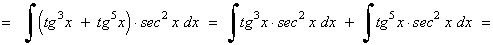
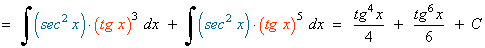
La potencia de la tangente es impar y positiva (2m+1) conservamos un factor de sec x·tg x y se usa la fórmula tg2x = sec2x - 1 para expresar los demás factores en términos de sec x :
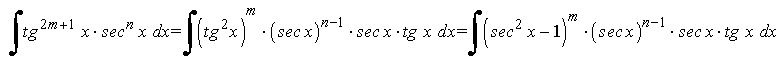
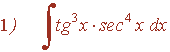
![]()
![]()
![]()
La potencia de la tangente es impar y positiva (2m+1) conservamos un factor de sec x·tg x y se usa la fórmula tg2x = sec2x - 1 para expresar los demás factores en términos de sec x :
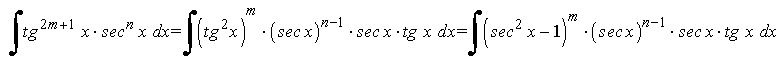
Ejemplo:
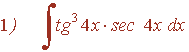
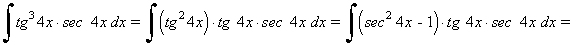
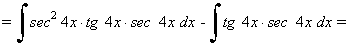
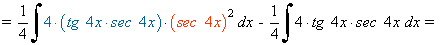
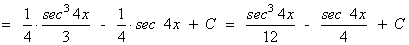
La potencia de la tangente es par y positiva (2m) y no hay secante convertimos un factor tg2x en términos de sec2x . Se desarrolla y se repite si es necesario:
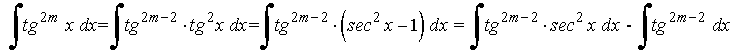
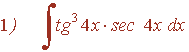
![]()
![]()
![]()
![]()
La potencia de la tangente es par y positiva (2m) y no hay secante convertimos un factor tg2x en términos de sec2x . Se desarrolla y se repite si es necesario:
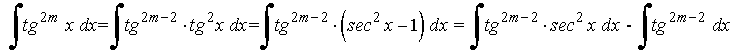
Ejemplo:
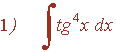
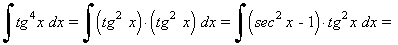
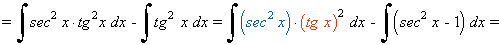
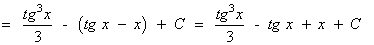
La potencia de la tangente es impar y positiva (2m+1) y no hay secante convertimos un factor tg2x en términos de sec2x . Se desarrolla y se repite si es necesario:
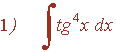
![]()
![]()
![]()
La potencia de la tangente es impar y positiva (2m+1) y no hay secante convertimos un factor tg2x en términos de sec2x . Se desarrolla y se repite si es necesario:
Ejemplo:
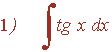
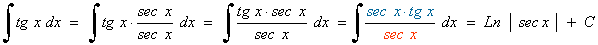
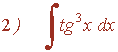
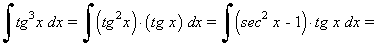
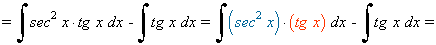
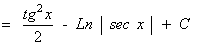
La potencia de la secante es impar y positiva (2n+1) y no hay tangente se resuelve por partes:
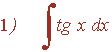
![]()
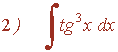
![]()
![]()
![]()
La potencia de la secante es impar y positiva (2n+1) y no hay tangente se resuelve por partes:


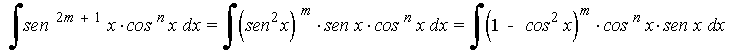
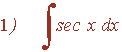
No hay comentarios:
Publicar un comentario