2.1. AREAS ENTRE CURVAS

UNIDAD 3: APLICACIONES DE LA INTEGRAL

3.1 AREAS ENTRE CURVAS

Supongamos que f (x) y g(x) sean funciones continuas en un intervalo cerrado [a, b] tal que f (x) ≥ g(x) en [a, b]. Queremos encontrar el área entre las gráficas de las funciones, como se muestra en la siguiente figura.

Figura 6.1_1  El área entre las gráficas de dos funciones, f (x) y g (x), en el intervalo [a, b].

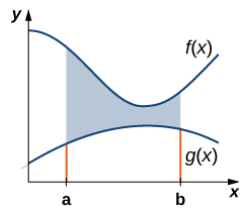
Como lo hicimos antes, vamos a dividir el intervalo en el eje x y aproximar el área entre las gráficas de las funciones con rectángulos. Entonces, para i = 0, 1, 2, …, n, sea P = {xi} una partición regular de [a, b]. Luego, para i = 1, 2, …, n, elija un punto xi* ∈ [xi − 1, xi], y en cada intervalo [xi − 1, xi] construya un rectángulo que se extienda verticalmente desde g (xi*) a f (xi*). La figura 6.2 (a) muestra los rectángulos cuando xi* se selecciona como el punto final izquierdo del intervalo con n = 10. La figura 6.2 (b) muestra un rectángulo representativo en detalle.

Figura 6.1_2 (a) Podemos aproximar el área entre las gráficas de dos funciones, f (x) y g (x), con rectángulos. (b) El área de un rectángulo típico va de una curva a otra.

La altura de cada rectángulo individual es f (xi*) − g (xi*) y el ancho de cada rectángulo es Δx. Agregando las áreas de todos los rectángulos, vemos que el área entre las curvas se aproxima por

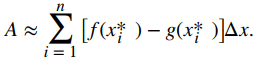
Esta es una suma de Riemann, entonces tomamos el límite cuando n → ∞ y obtenemos

Estos hallazgos se resumen en el siguiente teorema.

3.2. VOLUMENES DE SOLIDOS DE REVOLUCION

En este apartado podrás encontrar algunas aplicaciones de la integral, relacionadas con los volúmenes contenidos al rotar la gráfica de una función definida en un intervalo cerrado [a,b], alrededor de uno de los ejes y que son los llamados sólidos de revolución. En este trabajo los ejemplos serán de rotaciones alrededor del eje de las x. Por ejemplo, imagina una función constante en [0,2], al rotarla alrededor del eje x, se formaría un cilindro, pero si la función fuese la idéntica tendríamos un cono.

Objetivo

Calcular los volúmenes contenidos al rotar la gráfica de una función definida en un intervalo cerrado [a,b].

Conceptos previos

• Es de suma importancia tener en cuenta el corolario del Teorema Fundamental del Cálculo que dice:

• La fórmula para calcular el volumen del sólido de revolución al rotar una función definida en el intervalo [a,b], alrededor del eje de las x es .

• Sólo por dar una idea, diremos que dicha fórmula se obtiene considerando que el radio en cada corte circular es el valor de . El procedimiento de cálculo integral, utiliza límites de sumas de volúmenes de pequeñas arandelas o cortes circulares infinitesimales del sólido de revolución.

• Por un método similar, conocido como de capas cilíndricas, se obtiene la fórmula para rotaciones alrededor del eje de las y, a saber: .

Ejemplos

A continuación podrás ver algunos ejemplos de aplicaciones de la integral en el cálculo de volúmenes de sólidos de revolución. Para el cálculo de las integrales, consultaremos las tablas de integrales y en caso de que lo amerite, exhibiremos el procedimiento en una ventana flotante.

Da clic en un ejemplo, ejecútalo y si gustas reiniciar, da clic en el icono 

3.3. METODOS DE ARANDELAS Y CASCARAS CILINDRICAS

Nuevamente, estamos trabajando con un sólido de revolución. Como antes, definimos una región R, acotada arriba por la gráfica de una función y = f (x), abajo por el eje x y a la izquierda y derecha por las rectas x = a y x = b, respectivamente, como se muestra en la Figura 6.9 (a). Luego giramos esta región alrededor del eje y, como se muestra en la Figura 6.9 (b). Tenga en cuenta que esto es diferente de lo que hemos hecho antes. Anteriormente, las regiones definidas en términos de funciones de x giraban alrededor del eje x o una línea paralela a él.

Figura 6.9 (a) Una región delimitada por la gráfica de una función de x. (b) El sólido de revolución formado cuando la región gira alrededor del eje y.

Como lo hemos hecho muchas veces antes, “particionamos” el intervalo cerrado [a, b] usando una partición regular, P = {x0, x1, …, xn} y, para i = 1, 2, …, n, elija un punto xi* ∈ [xi − 1, xi]. Luego, construya un rectángulo sobre el intervalo [xi − 1, xi] de altura f (xi*) y ancho Δx. Un rectángulo representativo se muestra en la Figura 6.10 (a). Cuando ese rectángulo gira alrededor del eje y, en lugar de un disco o una arandela, obtenemos una cáscara cilíndrica, como se muestra en la siguiente figura.

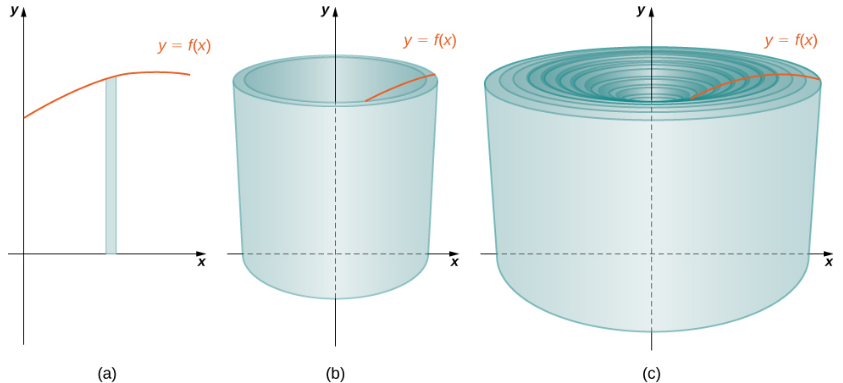
Figura 6.10 (a) Un rectángulo representativo. (b) Cuando este rectángulo gira alrededor del eje y, el resultado es una cáscara cilíndrica. (c) Cuando juntamos todas las capas, obtenemos una aproximación del sólido original.

Para calcular el volumen de este caparazón (carcasa, cáscara), considere la Figura 6.11.

Figura 6.11  Cálculo del volumen de la cáscara.

La carcasa es un cilindro, por lo que su volumen es el área de la sección transversal multiplicada por la altura del cilindro. Las secciones transversales son anillos (regiones en forma de anillo, esencialmente círculos con un orificio en el centro), con radio externo xi y radio interno xi − 1. Por lo tanto, el área de la sección transversal es

La altura del cilindro es f (xi*). Entonces el volumen V del caparazón es

Tenga en cuenta que si xi − xi − 1 = Δx, entonces tenemos

Además, (xi − xi − 1)/2 es tanto el punto medio del intervalo [xi − 1, xi] como el radio promedio del cascarón, y podemos aproximar esto por xi*. Entonces tenemos

Otra forma de pensar en esto es imaginar en hacer un corte vertical en el caparazón y luego abrirlo para formar una placa plana (Figura 6.12).

Figura 6.12 (a) Haga un corte vertical en una carcasa representativa. (b) Abra la carcasa para formar una placa plana.

En realidad, el radio exterior de la carcasa es mayor que el radio interior y, por lo tanto, el borde posterior de la placa sería ligeramente más largo que el borde frontal de la placa. Sin embargo, podemos aproximar la carcasa aplanada por una placa plana de altura f (xi*), ancho 2π xi* y espesor Δx (Figura 6.12). El volumen de la carcasa, entonces, es aproximadamente el volumen de la placa plana. Multiplicando la altura, el ancho y la profundidad de la placa, obtenemos

que es la misma fórmula que teníamos antes.

Para calcular el volumen de todo el sólido, agregamos los volúmenes de todas las capas y obtenemos

Aquí tenemos otra suma de Riemann, esta vez para la función 2πx f(x). Tomar el límite cuando n → ∞ nos da

Esto lleva a la siguiente regla para el método de las capas cilíndricas.

3.4. LONGITUD DE ARCO

Usualmente medimos la longitud con una línea recta, pero las curvas también tienen longitud. Un ejemplo familiar es la circunferencia de un círculo de radio $r$r, cuya longitud es $2\pi r$2, pi, r. En general, le llamamos a la longitud de una curva "longitud de arco". Pero, ¿cómo encuentras la longitud de arco de una curva arbitraria? Averigüémoslo.

Qué vamos a construir

• Puedes encontrar la longitud de arco de una curva con una integral que se ve como algo así:

  $\displaystyle \int \sqrt{(dx)^2 + (dy)^2}$integral, square root of, left parenthesis, d, x, right parenthesis, squared, plus, left parenthesis, d, y, right parenthesis, squared, end square root

  Los límites de esta integral dependen de cómo defines la curva.
• Si la curva es la gráfica de una función, $y = f(x)$y, equals, f, left parenthesis, x, right parenthesis, reemplaza el término $dy$d, y en la integral con $f'(x)dx$f, prime, left parenthesis, x, right parenthesis, d, x y luego factoriza el término $dx$d, x.

Calentamiento: aproximar la longitud de arco

Echemos un vistazo a la parábola definida por la siguiente ecuación:

$y = f(x)= x^2$y, equals, f, left parenthesis, x, right parenthesis, equals, x, squared

Considera la porción de la curva que está entre $x = -2$x, equals, minus, 2 y $x = 2$x, equals, 2.

$\small{1}$$\small{2}$$\small{3}$$\small{4}$$\small{\llap{-}1}$$\small{\llap{-}2}$$\small{\llap{-}3}$$\small{\llap{-}4}$$\small{1}$$\small{2}$$\small{3}$$\small{4}$$\small{\llap{-}1}$$\small{\llap{-}2}$$\small{\llap{-}3}$$\small{\llap{-}4}$$y$$x$

Solo para que quede clara la pregunta, imagina que la curva es un pedazo de cuerda, y que la estiras y mides su longitud con una regla.

3.5. AREA SUPERFICIAL DE UN SOLIDO EN REVOLUCION

Imagina una función constante en [0,2], al rotarla alrededor del eje x, se formaría un cilindro, pero si la función fuese la idéntica tendríamos un cono. En el apartado anterior calculamos el volumen generado, ahora calcularemos las áreas de las superficies generadas.

Objetivo

Calcular las áreas de las superficies generadas al rotar la gráfica de una función definida en un intervalo cerrado [a,b].

Conceptos previos

• Es de suma importancia tener en cuenta el corolario del Teorema Fundamental del Cálculo que dice:

• La fórmula para calcular el área de una superficie de revolución al rotar una función definida en el intervalo [a,b], alrededor del eje de las x está dada por:

• Sólo por dar una idea, diremos que dicha fórmula se obtiene considerando que el radio en cada corte circular es el valor de  y por lo tanto cualquiera circunferencia tendría un perímetro igual a , pero habrá que considerar esta medida a lo largo de toda la curva. El procedimiento formal de cálculo integral, utiliza límites de sumas de áreas de pequeñas arandelas o cortes circulares infinitesimales de la superficie de revolución, a lo largo de toda la curva.

• Por ello en la fórmula aparece la expresión de la longitud de arco, puesto que para calcular toda el área, es necesario recorrer toda la curva.

Ejemplos

A continuación podrás ver algunos ejemplos de aplicaciones de la integral en el cálculo de áreas de superficies de revolución. Para el cálculo de las integrales, consultaremos las tablas de integrales y en caso de que lo amerite, exhibiremos el procedimiento en una ventana flotante.

Da clic en un ejemplo, ejecútalo y si gustas volverlo a ejecutar, da clic en el icono de reiniciar 

3.6. DENSIDAD DE LA MASA 

La masa de un cuerpo y el volumen que este ocupa están relacionadas por un concepto llamado densidad.  Imagina ahora que tomamos una pelota de metal lo suficientemente pequeña para que tenga la misma masa que la de goma, si las ponemos en la bascula, la aguja marcará lo mismo para las dos.

La esfera de metal tiene ahora la misma masa que la de goma pero ocupa mucho menos volumen, por esto se dice que es más densa.  La densidad de un objeto se obtiene haciendo la división de su masa entre el volumen que ocupa.  Así por ejemplo, si un objeto pesa  gramos y ocupa un volumen de  centímetros cúbicos su densidad será de  gramos por cada centímetro cúbico:

A la hora de medir la densidad hay que tener en cuenta las condiciones a las que se ve sometido el objeto, pues estas pueden cambiar sus propiedades físicas.  La temperatura por ejemplo, aumenta el volumen de muchas cosas.  Si mides la densidad de una barra de metal a temperatura ambiente, será mayor que si la mides después de calentarla, pues la temperatura aplicada hará que la barra ocupe más espacio, aumentando su volumen.

3.7. CENTROS DE MASAS Y MOMENTOS

 DE INERCIA

El centro de masas y el momento de inercia son propiedades geométricas, no dependientes de ningún otro parámetro y de gran importancia a la hora de diseñar ciertas estructuras o componentes. Ambos están relacionados en el sentido de que en muchos casos para calcular la inercia (sobre todo en figuras compuestas por varios rectángulos) es necesario conocer el centro de masas para aplicar el Teorema de Steiner.

Momentos de Inercia

Inercia es una palabra que utilizamos demasiado a menudo de forma que según la RAE, la inercia es:

1. f. Mec. Propiedad de los cuerpos de no modificar su estado de reposo o movimiento si no es por la acción de una fuerza.

Por ejemplo cuando empujamos algo que se mueve linealmente, solemos decir que tiene mucha inercia. Sin embargo, esto no es del todo correcto puesto que la inercia es, estrictamente hablando, la resistencia a los cambios en la rotación de un objeto.

La inercia puede calcularse mediante la el producto masa por distancia al cuadrado, o en caso de tratarse de una densidad constante y para una geometría continua, de la manera siguiente:

3.8. TRABAJO

l concepto de trabajo, en Física, está íntimamente relacionado con las transformaciones que sufren los cuerpos. De entre todas ellas, una de las más evidentes y cómodas de estudiar es la de las transformaciones mecánicas (las transformaciones en el estado de movimiento de un cuerpo). En este apartado vamos a introducir el trabajo tal y como lo entendemos en Física, centrándonos sobre todo en un tipo de trabajo específico denominado trabajo mecánico.

Por otro lado, en apartados anteriores introdujimos el concepto de fuerza y el de desplazamiento. En este apartado supondremos un punto material que se desplaza en linea recta sobre el que actúa una fuerza constante.

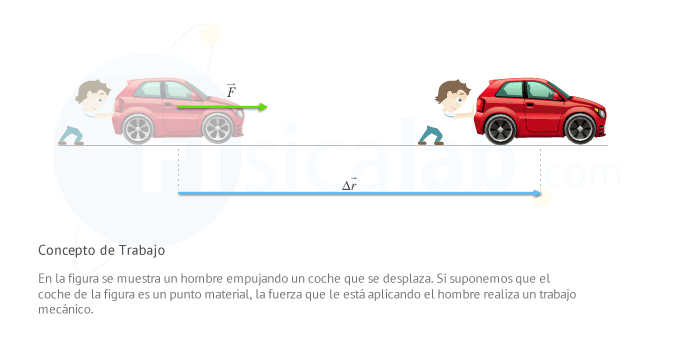
Definimos trabajo realizado por una fuerza constante que actúa sobre un cuerpo que se mueve con movimiento rectilíneo como el producto escalar de la fuerza por el desplazamiento:

W=F→⋅Δr→=F⋅Δr⋅cosϕ=F⋅Δs⋅cosϕ

Donde:

• W es el trabajo realizado por la fuerza. Su unidad de medida en el Sistema Internacional es el Julio (J).
• F es una fuerza constante. Su unidad de medida en el Sistema Internacional es el Newton (N).
• Δr→ es el vector desplazamiento del cuerpo. Su unidad de medida en el Sistema Internacional es el metro.
• Δs es el espacio recorrido por el cuerpo. Dado que el movimiento es rectilíneo, coincide con el módulo del vector desplazamiento Δr .Su unidad de medida en el Sistema Internacional es el metro.
• ϕ es el ángulo que forman las fuerza y el desplazamiento experimentado por el cuerpo. Su unidad de medida en el Sistema Internacional es el radián (rad).

Observa como coinciden, por tratarse de un movimiento rectilíneo, el módulo del  vector desplazamiento Δr y el espacio recorrido Δs .

3.9. FUERZA Y PRESION

¿Qué significa la presión?

Si trataras de usar un martillo para clavar un pino de boliche a una pared, probablemente no pasaría nada, excepto que las personas dejarían de prestarte sus pinos de boliche. Sin embargo, si usaras un martillo para clavar un clavo con la misma fuerza, es más probable que entre en la pared. Esto muestra que algunas veces no es suficiente con solo saber la magnitud de la fuerza: también tienes que saber cómo está distribuida esa fuerza en la superficie de impacto. Para el clavo, toda la fuerza entre la pared y el clavo está concentrada en la pequeña área de su punta afilada. Para el pino de boliche, el área en contacto con la pared es mucho mayor y la fuerza está mucho menos concentrada.

Una persona que golpea un pino de boliche y un clavo con un martillo.

Para precisar este concepto, utilizamos la idea de presión. Definimos la presión como la cantidad de fuerza ejercida por unidad de área.

${\Large P=\dfrac{F}{A}}$P, equals, start fraction, F, divided by, A, end fraction

Así que para crear una gran cantidad de presión, puedes ejercer una fuerza muy grande o ejercer una fuerza sobre un área pequeña (o ambas). En otras palabras, puedes permanecer seguro recostado en una cama de clavos si el área superficial total de las puntas de los clavos es lo suficientemente grande.

El peso de la columna de agua sobre la lata de frijoles crea una presión en la parte superior de la lata. Para determinar una expresión para la presión, comenzaremos con la definición de presión.

$\Large P=\dfrac{F}{A}$P, equals, start fraction, F, divided by, A, end fraction

Para la fuerza $F$F, debemos sustituir el peso de la columna de agua sobre la lata de frijoles. El peso siempre lo encontramos con la expresión $W=mg$W, equals, m, g, así que podemos escribir el peso de la columna de agua como $W=m_{a}g$W, equals, m, start subscript, a, end subscript, g, donde $m_a$m, start subscript, a, end subscript es la masa de la columna de agua sobre los frijoles. Al sustituir esta expresión en la ecuación para la presión, obtenemos

$P=\dfrac{m_a g}{A}$

3.10. FORMAS INDETERMINADAS Y LA

 REGLA DE L' HOSPITAL

El límite


es una forma indeterminada 0/0, pues tanto el numerador como el
denominador tienden a 0 cuando 

x tiende a 0.  Este límite no puede ser
determinado usando operaciones algebraicas que permitan la cancelación de
factores del numerador y denominador. Éste  junto con otros límites de
cocientes que son formas indeterminadas 0/0 o infinito sobre infinito pueden
ser evaluado aplicando la regla de l´Hôpital,  calculado el límite del cociente
de  las derivadas.

Extensiones de la regla de l´Hôpital.
La regla se sigue cumpliendo en el caso que se tenga una forma indeterminada del tipo infinito sobre infinito. Esto es si

        

También se cumple para límites laterales, es decir, si c es sustituido por c ⁺ o c ^-,

Finalmente, se cumple para límites en el infinito, c por ∞.

3.11. INTEGRALES IMPROPIAS